Products

home>products>미국 nanoComposix 제품>플라즈모닉 나노입자(Plasmonic Nanoparticles)



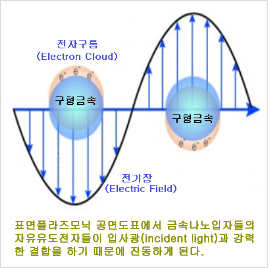플라즈모닉 나노입자들은 (일반적으로 10-150 nm 직경의 금 및 은 입자들) 높은 효율의 광 흡수 및 광분산을 가지는 금속나노 입자들이다. 입자 크기, 형태, 표면 코팅등을 바꿔주면 전자기스펙트럼(electromagnetic spectrum)의 가시광선에서 근적외선 영역에 이르기까지 나노입자들의 색(color)을 조절할수 있다.

구형 금나노 입자들의 용액은 스펙트럼의 녹색(green)영역에서 강한 분산과 흡수가 일어나기 때문에 색상이 루비 빨강(Ruby Red) 이다. 은나노 입자들의 용액은 스펙트럼의 파랑(blue) 영역에서 플라즈모닉 공명이 일어나기 때문에 노란색(Yellow) 으로 보인다.(빨강(Red) 및 녹색(Green) 광 영향을 받지 않는다).

금 및 은 나노입자들의 고유의 분광학적 반응의 이유는 빛의 비파장(specific wavelength)이 표면플라즈몬공명(SPR)으로 알려진 금속의 유도전자들의 집단적으로 진동을 일어나게 하기 때문이다.
이러한 공명이 여기(Exited)하면, 공명하지 않는 같은크기의 입자들보다 흡수 및 분산세기(Intensities)가 최대 40배에 이를수 있다.
플라즈모닉 나노입자들의 광학적특성의 밝기 및 조절성(tunabilities)은 분자검출(molecular detection), 솔라 에너지 물질, 그리고 암발견 및 치료등의 다양한 분야에의 적용성을 아주 높게 만든다.

[플라즈모닉 해설(Plasmonics Tutorial)]

 귀금속 나노입자들은 다른종류의 물질에서는 보여지지않는 특별한 광학적 특성을 가져오는 표면 플라즈몬(나노입자 표면에서의 유도전자의 진동)을 확실히 보여준다. 그 효과의 기본은 금속나노입자에서의 자유전자의 플라즈몬공명이며, 분극율(polarizability)을 연구하므로서 이해될수 있다.(금속나노입자 표면의 유도전자, 전하분포 및 부분 쌍극자 형태의 영향등 전하를 가지고하면 쉽다).
구형 나노입자들에서 , 나노입자들의 준-정적분극율(quasi-static polarizability)은 다음과 같이 주어진다.


여기서 ε1 은 나노입자들의 파장종속유전함수(wavelength dependent dielectric function)이고 ε2는 파장과는 상관없는 거의 일정하게 유지되는 중간체(medium)의 유전함수(dielectric function) 이다.
조건 Re{ ε 1 } = -2 ε 2 이 만족한다면, 그 입자들은 그값의 파장에서 흡수 및(혹은) 분산의 강력한 증가를 가져오는 공명을 하게된다. 공명조건은 나노입자들의 파장종속유전함수(wavelength dependent dielectric function)뿐만 아니라 중간체(medium)의 유전함수에도 의존한다. 따라서, 나노입자의 광특성은 물질의 구성, 크기, 및 입자들을 함유하고있는 중간체등에 아주 많이 의존한다.

나노 입자 플라즈몬 공명의 모양 및 최대공명 파장 모두는 부분 굴절율(Local refractive index)에 의해 영향을 받는다. 입자들이 물에있을때(n=1.33), 80nm 은 입자의 최대공명은 Mie 이론(Mie Theory)에 의해 ~445nm 로 예상된다. 공기에서(n=1.00) 플라즈몬 공명의 최대파장은 ~380nm, 65nm 의 청색이동(Blue-shift)로 예상 된다. 그러나 , 만약에 은입자가 물과 똑같은 굴절율을 가지는 물질의 쉘로 코팅이 된다면, 그 최대 플라즈몬 파장은 ~445nm 로 복구될 것이다. 쉘의 두께를 조절함으로, 코팅된 나노입자들의 최대 공명이 이러한 두 개의 말단값(380nm~445nm)의 사이에서 어떤파장으로도 조절되어 질수 있다. 다른 입자 크기, 구성 및 굴절률들에서도 이러한 효과를 관찰하려면, 당사의 온라인 Mie 이론 시물레이터(Online Mie Theory Simulator-OMTS)를 보면 금 및 은나노 입자들의 이론적인 광학 반응을 계산하고 볼수 있을 것이다.
나노 입자들의 광학적 특성들은 다른 플라즈모닉 물질들이 근접해 있으면 아주 민감하다. 두 개 혹은 그이상의 플라스모닉 나노입자들이 가까이에 있으면(입자 하나의 직경이나 그직경보다 더작은 절단 분리(edge-to-edge separations)를 가진), 그들의 표면 플라스모닉 결합들은 각각의 입자들의 유도전자로서 집합적으로 진동한다. 이 효과는 분자 궤도 이론(Molecular orbital theory)와 비슷해서, 결합된입자들의 플라스몬 공명 파장이 더 긴파장(더 낮은 에너지)으로 빨강-이동(Red Shift)을 하기 때문에 ,그 플라즈몬 결합에서 진동하는 전자가 낮은 에너지 상태에 있다고 추정되는 결과를 보인다. 이러한 결합효과는 나노입자들이 응집되고 또한 많은 다른 형태의 플라스모닉 나노입자 센서들을 주구성 요소로 할때 이러한 결합효과는 플라스모닉 나노입자 용액들의 보이는색상의 극적인 변화에 대한 원인 이다.

[플라즈모닉 나노입자의 광특성 모델링(Plasmonic Nanoparticle Optical Properties)]
◎ Mie 이론(Mie Theory)
Mie 이론은 실질적으로 이론이 아니고, 차라리 구형 입자에 의한 빛의 분산에 대한 맥스웰 방정식(Maxwell's equations) 의 분석적인 해법이다. Mie 이론은 어떤 파장의 빛에서 어떤 직경을 가진 구형 입자들로 부터의 분산을 계산하는데 사용될수 있다. 고전적인 Mie 이론은 그 구형 입자가 단일물질로 이루어졌다고 추정을 한 반면에, 좀더 최근에는, 층을 이룬 구형입자들로부터의 빛의 분산을 풀기위해 적용되었다.
nanoComposix에서, 우리는 금속, 및 나노입자 유전체 와 마이크로 입자 유전체로 부터의 소멸, 흡수,분산을 계산하기위한 맞춤의 Mie 이론 코드(Custom Mie theory Code)를 집필하였다.
◎ 이산 쌍극자 근사법(Discrete Dipole Approximation)
Mie 이론은 단지 구형입자들로부터의 빛의 분산을 계산하는데 사용될수 있고, 구형이 안닌 입자들의 빛의 분산을 계산하기위해서 다른 이론이 필요하다.
맥스웰 방정식으로의 분석적 해법은 모든 형태의 계산에 사용될 수 없고, 이산 쌍극자 근사법(Discrete Dipole Approximation)과 같은 대체방법으로 다른 입자형태의 소멸, 흡수, 분산을 계산하는데 사용된다.
이산 쌍극자 근사법에서는, 입자들을 계산 유체 역학의 이차원 격자(2-D grid) 나 메쉬로 만들어 사용하는것과 비슷한 방법으로 극성화할수 있는 입방체의 묶음으로 세분할(subdivided) 한다. 각각의 입방체의 중심에서 두 개의 입사광 으로의 단일 쌍극 및 각각의 다른 입방체들로부터 분산된 빛의 반응을 계산하는것에 의해 빛에대한 반응을 계산한다.
이러한 반복적인 과정은 나노입자들의 형태 및 크기 그리고 입방체 격자(Cubic grid)의 크기에 따라 꽤 많은 계산시간이 필요할 수 있다.
◎ 왜 모델링을 하나(Why model?)
모델링은 주어진 크키 및 형태의 나노 입자들의 광학 특성을 예상하는데 사용될수 있다.
예를들면, 우리는 길이 및 길이:폭비율에 상관되는 광학적 특성을 가진 금나노막대의 합성 방법을 발전 시켜왔다. 제조 공정에서 길이 및 폭을 조절할수 있기 때문에, 모델링은 원하는 파장(즉, 특정한 선명한 선-specific laser line) 에서 공명할 수 있는 목표 형태를 선택하는데 사용될수 있다.

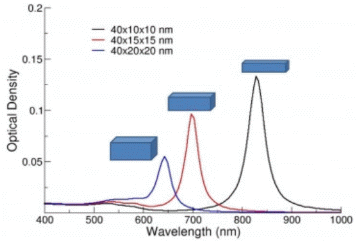<다양한 면비의 금나노막대의 수학적으로 모델링된 스펙트럼>

우리는 또한, 모델링을 품질을 조절하는데에 사용한다(QC). 나노 입자들을 제조한후에, 입자의 크기는 전자현미경으로 특성화 되어지고, 측정된 광학적 효율은(광학적 밀도는 자외선가시분광법(UV-Visible spectroscopy)을 사용하여 측정되고 용액의 금속의 양에 의해 정해진다) Mie 이론 이나 DDA 시물레이션에서 결정된 광학적 효율과 비교를 한다.

80nm NanoXact 은(Blue) 및 금(Red)의 측정된값(dashed lines) 과 이론적인값의 (solid lines) 광학효율 이 아래의 그림에 나와 있다. 측정된 광학 효율은 이론값의 최대 2% 이내에 있어, 입자들이 고도로 단분산 되어 있으며 일정한 구 형태를 가지고 있음을 입증한다.

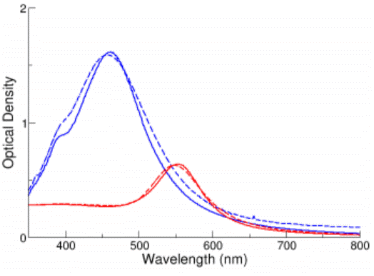<80nm 금 및 은 BioPure 나노 입자들의 측정된(Dashed) 값과
수학적으로 모델링된(Solid) 소멸 스펙트럼 비교>